Tytuł. Kliknij na mnie dwukrotnie.
E-PORTFOLIO
Tytuł. Kliknij na mnie dwukrotnie.

E-PORTFOLIO

ZADANIA ARCHIWALNE
KLASA 6
KLASA 7
Zad. 4
Motocyklista w ciągu 7/12 godziny przejechał 7/15 zaplanowanej trasy.
Jaką drogę zaplanował do przejechania motocyklista, jeżeli jechał ze średnią prędkością 69,6 km/h?
Zad. 1
W szkolnym rajdzie brała udział cała klasa VIB. W drodze doszło jednak do
nieporozumień i uczestnicy podzielili się na dwie grupy. Gdyby Zosia przeszła
z grupy pierwszej do drugiej, to w pierwszej grupie byłaby jedna trzecia klasy.
Gdyby Adam, Marek i Wojtek przeszli z grupy drugiej do pierwszej, to w grupie
tej znalazłaby się połowa klasy. Ilu uczniów jest w klasie VIB?
Zad. 2
Numer pewnej sali lekcyjnej jest liczbą 3-cyfrową, której suma cyfr wynosi 10,
cyfra setek stanowi 0,6 cyfry dziesiątek, a cyfra jedności jest 4 razy mniejsza od sumy cyfry setek i dziesiątek. Jaki numer ma ta sala?
Zad. 1
Do suszenia przygotowano 4 kg grzybów. Na początku było w nich 3,5 kg wody, po pewnym czasie ilość wody zmniejszyła się o pół kilograma, a jeszcze później spadła do 1 kg. Jakim procentem masy grzybów była zawarta w nich woda - przed suszeniem i na każdym z opisanych etapów suszenia?
Zad. 3
Jeden z boków prostokąta zwiększono o 25%. O ile procent należy zmniejszyć drugi bok, aby pole prostokąta nie uległo zmianie?
Zad. 2
Sad owocowy ma kształt prostokąta, którego długości boków są w stosunku 2:7. Krótszy bok jest równy 240 metrów. W ciągu ilu dni obejdzie ten sad ślimak idący ze średnią prędkością 4 m/h?
Zad. 3
W pewnym prostokącie miara między przekątną a dłuższym bokiem stanowi 20% miary między tą przekątną a krótszym bokiem. O ile procent większa jest miara kąta rozwartego między przekątnymi od miary kąta ostrego między tymi przekątnymi?

Zad. 5
Zad. 4
Pan Zenon sprzedawał w październiku winogrona po 7,20 zł za kilogram,
a zysk z tej sprzedaży wynosił 20% ceny hurtowej. W listopadzie pan Zenon podwyższył cenę winogron tak, aby jego zysk wyniósł 44% ceny hurtowej.
O ile procent wzrosła cena winogron w sklepie pana Zenona, jeśli cena hurtowa
się nie zmieniła?
Zad. 5
W trapezie równoramiennym ABCD bok AB jest równoległy do boku CD.
Przekątna trapezu dzieli jego kąt ostry na kąty o równych miarach.
Z wierzchołka C kąta rozwartego poprowadzono wysokość CE. Ramię trapezu
ma 5 cm, EB = 3 cm, a pole trójkąta CEB wynosi 6 centymetrów kwadratowych.
Oblicz pole trapezu ABCD.
Zad. 6
Oblicz, jaki dzień tygodnia był 08.07.1969r., jeżeli 08.07.2000r.
wypadł w sobotę.
Zad. 6
W pewnej fabryce wyprodukowano 200 sztuk garnków w ciągu 15 dni, realizując 20% zamówienia. O ile procent należy zwiększyć produkcję, aby w ciągu następnych 50 dni zakończyć realizację zamówienia?
Zad. 7
Farmer sprzedał trzy owce i kupił dwie kozy, dokładając do transakcji
20 funtów. Następnie sprzedał dwie owce i kupił jedną kozę, w tej transakcji wychodząc na zero. Jaka była cena owcy? Ile kosztowała koza?
Zad. 7
Bartek dojeżdża do szkoły rowerem. Zawsze wyjeżdża o 7:55 i przyjeżdża
równo o 8:00. Pewnego dnia jechał z prędkością o 6 km/h mniejszą i spóźnił się
o 2 minuty. Jak daleko ma Bartek do szkoły?
Zad. 8
Krawędzie prostopadłościanu mają się do siebie jak 3:7:8. Pole powierzchni całkowitej jest równe 808 centymetrów kwadratowych. Oblicz długości krawędzi tej bryły.
Zad. 8
Marcin zobaczył Tomka w odległości 100 m. Chłopcy pobiegli jeden do drugiego, Marcin z prędkością 4 m/s, a Tomek z prędkością 5 m/s.
Po jakim czasie chłopcy spotkają się?
Zad. 9
Złotnik stopił 12 g stopu srebra próby 940 i 10,4 g stopu srebra próby 800.
Oblicz próbę otrzymanego stopu.
Zad. 9
Za pomocą trzech różnych cyfr parzystych zapisz wszystkie liczby czterocyfrowe niepodzielne przez 4 i mające sumę cyfr równą 26.
Zad. 10
Na koniec roku szkolnego średnia ocen w pewnej 28-osobowej klasie
wynosiła 4,25. Chłopców było o 4 mniej niż dziewcząt. Średnia ocen dziewcząt wynosiła . Jaka była średnia ocen chłopców?
Zad. 10
Długopis kosztuje o 60% mniej niż piórnik. Piórnik kosztuje o 60% mniej
niż plecak. O ile procent plecak jest droższy od długopisu?
Zad. 11
Smok Parabolus zjada tonę jedzenia w 20 minut. Jego synek Wielomianek zjada taką samą ilość w 1 godz. 40 min. Dziś na obiad mają pyszne
3-tonowe danie. W jakim czasie zjedzą je razem?
Zad. 11
Kolejka w lunaparku porusza się ze stałą prędkością po zamkniętym torze
o długości 60 m. Postanowiono zwiększyć prędkość kolejki o 0,4 km/h.
Wojtek zauważył, ze czas przejażdżki po zwiększeniu prędkości kolejki
nie zmienił się, za to wykonuje ona o jedno okrążenie więcej.
Ile minut trwa jedna przejażdżka kolejką?
Zad. 12
W trapezie równoramiennym ABCD boki AD, BC i CD mają jednakowe długości.
Przekątna AC jest prostopadła do BC. Oblicz miary kątów tego trapezu.
Zad. 12
Podstawę XY trójkąta równoramiennego XYZ przedłużono poza punkt X, obierając na tym przedłużeniu punkt A, a także poza punkt Y, obierając tam punkt B. Kąty ostre trójkątów AXZ i BYZ mają miary: 8°, 20°, 32°, 44° (nie wiadomo, która miara dotyczy którego kąta). Podaj miary kątów trójkąta XYZ.
Zad. 13
5555 niewolników zbudowało grobowiec w ciągu 1 roku i 2 miesięcy.
Jak szybko zbudowałoby ten grobowiec 7777 niewolników?
Zad. 13
W sadzie rosła grusza. Z jej pnia wyrastała pewna liczba konarów.
Z każdego konara wyrastało tyle gałęzi, ile było wszystkich konarów.
Na każdej gałęzi rosło dwa razy więcej gruszek, niż było wszystkich gałęzi na tym drzewie. Gruszek było 1250. Ile konarów wyrastało z pnia gruszy?
Zad. 14
Która jest obecnie godzina, jeżeli wiesz, że pozostała część doby stanowi 20%
części doby, która już minęła?
Zad. 14
Babcia Wanda przyniosła na targ 100 jajek, które chciała sprzedać za 32 zł.
Gdy sprzedała czwartą część wszystkich jajek, zauważyła, że część jajek jest popękanych. Odłożyła je na bok i aby zarobić ustalone 32 zł, resztę sprzedała
po 40 gr za sztukę. Oblicz, ile jajek było popękanych.

Zad. 15
Zad. 15
Dwie zielone kostki ważą o 10 g mniej niż jedna niebieska. Dwie kostki niebieskie ważą o 10 g mniej niż jedna biała. Dwie kostki białe ważą o 200 g więcej niż jedna zielona. Ile waży biała kostka?
Zad. 16.
Jeśli liczba K stanowi 0,1 liczby L, L stanowi 0,2 liczby M, M stanowi
0,3 liczby N, zaś P stanowi 0,4 liczby N, ile wynosi wówczas iloraz K:P ?
Zad. 16
W rodzinie Wojtka są cztery osoby. Suma ich lat jest równa 100. Wojtek jest
o 4 lata starszy od swojej siostry Asi, a tata jest o 6 lat starszy od mamy.
Asia poprosiła złotą rybkę, żeby cofnęła czas o całkowitą liczbę lat do takiego momentu, w którym Asia była 6 razy młodsza od mamy. Złota rybka chwilę się zastanowiła i cofnęła czas o 5 lat. Ile lat mają po cofnięciu czasu członkowie tej rodziny?
Zad. 17
Liczbę 180 podziel na takie dwie liczby, żeby pierwsza z nich stanowiła siedem trzynastych drugiej.
Zad. 17
Na parkingu stały samochody, wśród których 20% stanowiły samochody
ciężarowe, a 80% - osobowe. Po pewnym czasie odjechało 20% ciężarówek,
oraz 80% samochodów osobowych. Jaki procent samochodów, które pozostały
na parkingu, stanowią samochody ciężarowe, a jaki - osobowe?
Zad. 18
Obwód prostokątnego sadu jest równy 150 m. Długości boków sadu są
w stosunku 3:2. Jaką powierzchnię zajmuje ten sad i ile w nim posadzono
drzew, jeżeli na jedno drzewo zaplanowano 4,5 metra kwadratowego?
Zad. 18
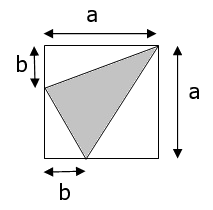
Zapisz pole zacieniowanego trójkąta w postaci
wyrażenia algebraicznego. Uprość zapisane wyrażenie,
a następnie oblicz to pole dla a = 5 cm i b = 1 cm.